FWT 学习笔记

想尽量讲得本质一点。

首先有一个引出问题叫做 集合幂级数

\[c_i=\sum_{j \ opt\ k=i}a_jb_k \]

其中，$opt$ 是集合的并交补运算，而 $i,j,k$ 也都是集合的意思

当我们把 $i,j,k$ 看成二进制表示，那么集合中的每一个元素的选/不选对应二进制的 $1/0$ ， $opt$ 变成了 $or,and,xor$ 的一种

所以问题变成了这样：给定两个长度为 $2^n$ 的序列 $a_i,b_i$ （不够长用 $0$ 补全），求出一个序列 $c$ ，满足 $\forall i,c_i=\sum_{j \ opt\ k=i}a_jb_k$

这个时候我们可以使用，FWT ，$\text{Fast Walsh-Hadamard Transform}$ ，快速沃尔什变换。

FFT

发现 $fwt$ 和 $fft$ 的英文很像，所以我们考虑，类似的思路

关于 $fft$ ，我们有一个经典思路是：（图源：pyb 的 ppt)

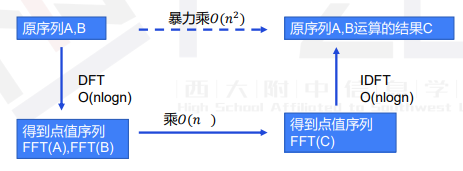
其中，我们能做到 $O(n\log n)$ 的 $DFT$ 的原因在于我们有两个重要操作叫做 奇偶分段蝴蝶变换 ，也就是说我们把原来的东西进行分治的操作后可以 $O(1)$ 的合并回去，$O(n\log n)$ 的 $IDFT$ 在于一个 $w$ 的性质的应用，我们不妨尝试把这样的思想套进 FWT

记住上图！

FWT

现在我们有这样的目标：找到一种变换 $FWT$ ，使得

\[FWT(A)\times FWT(B)=FWT(C) \]

其中，$\times$ 表示对应位相乘，然后通过 $FWT(C)$ 复原 $C$

显然，我们的 FWT 应该是对于原序列的一种线性组合，即某一项只是若干个原多项式中的若干项的若干倍的和

因为我们本来的 $c_i$ 就是数个 $a_jb_k$ 的和，而 FWT 是对应位相乘，如果其出现原多项式某几项的乘积，那么显然 GG

所以显然有的是 $FWT(A+B)=FWT(A)+FWT(B)$

这里不妨约定一些记号:

$ 𝐴 = 𝑎_𝑖 ,𝐵 = 𝑏_𝑖 , 𝐶 = 𝑐_𝑖 $

$ 𝐴 + 𝐵 = 𝑎_0 + 𝑏_0, 𝑎_1 + 𝑏_1,\dots $

$ 𝐴 − 𝐵 = 𝑎_0 − 𝑏_0, 𝑎_1 − 𝑏_1,\dots$

$ 𝐴\oplus𝐵 = \sum_{𝑖⨁𝑗=0} 𝑎_𝑖 ∗ 𝑏_𝑗 , \sum_{𝑖⨁𝑗=1} 𝑎_𝑖 ∗ 𝑏_𝑗 ,\dots$

默认所有的数列都有 $2^n$ 项，即可以理解为集合元素个数有 $𝑛$ 个

$ 𝐴_0$ 代表数列 $𝐴$ 的前 $2^{𝑛−1}$ 项，即最高位（第一个）不选的所有集合，$𝐴_1$ 代表数列 $𝐴$ 中的后 $2 ^{𝑛−1}$ ，即最高位（第一个）选的所有集合

FWTor

假设现在我们的 $opt$ 就是 $or$ ，下面简记 $A|B=\sum_{j|k=i} a_jb_k$

下面讲得可能有点小乱

FWT

总体想法是仿照 FFT ，考虑一个递归的形式构造出 FWT

显然，当 $n=0$ 的时候，$FWT(A)=A$

下面讨论 $n>0$ 的情况，我们首先考虑奇偶分段，假装我们已经知道了 $FWT(A_0),FWT(A_1)$

于是，一个粗略的 FWT 出现了： $FWT(A)=Merge(FWT(A_0),FWT(A_1))$

$Merge$ 表示直接拼接，xjb 举一个例子：$Merge(998,244)=998244$

我们知道 $FWT(C)$ 需要等于 $FWT(A)\times FWT(B)$

还知道 $C_0=A_0B_0$ ,$ C_1=A_0B_1+A_1B_0+A_1 B_1$

发现上面那个显然不靠谱，我们对应位相乘后，只会得到 $FWT(C_0)=FWT(A_0)FWT(B_0),FWT(C_1)=FWT(A_1)FWT(B_1)$ 这样一个错误。

也就是说后半部分还需要有 $FWT(A_0)$ 的信息甩进去，所以：（这里不妨将 FWT 当成一个神秘的抽象函数）

\[FWT(A)= \begin{cases} Merge(FWT(A_0),FWT(A_0)+FWT(A_1))&,n>0\\ \quad \quad\quad\quad\quad\quad\quad\quad A&,n=0 \end{cases} \]

（回顾 $+$ 的记号：$ 𝐴 + 𝐵 = 𝑎_0 + 𝑏_0, 𝑎_1 + 𝑏_1,\dots $）

可是这样还是有问题呀，这样对应位相乘，好像会多一个 $FWT(A_0)FWT(B_0)$ 项的贡献出现在 $FWT(C_1)$ 中

但值得注意的是， $FWT(C)$ 并不一定需要就是 $C$ 了，我们不妨将这个问题交给 $IFWT$ 处理，

至少我们这里保证了信息是完全的，并且符合我们心目中奇偶分段和蝴蝶变换的要求

也就是说像这样给出来后，IFWT 有操作空间，并且 FWT 时间的确是 $n\log n$

当然，我们还需要保证 $FWT(A)\times FWT(B)=FWT(C)$

这里采用类似数学归纳法的方式证明，思路来自 pyb 的 ppt ，

即假设已知 $FWT(A_0)\times FWT(B_0)=FWT(C_0),FWT(A_0)FWT(B_1)+FWT(A_1)FWT(B_0),FWT(A_1)FWT(B_1)=FWT(C_1)$ ，那么

\[\begin{align} FWT(A)\times FWT(B)&=Merge(FWT(A_0),FWT(A_0+A_1))\times Merge(FWT(B_0),FWT(B_0+B_1))\\ &=Merge(FWT(A_0)FWT(B_0),FWT(A_0)FWT(B_0)+FWT(A_0)FWT(B_1)+FWT(A_1)FWT(B_0),FWT(A_1)FWT(B_1))\\ &=Merge(FWT(A_0B_0),FWT(A_0B_0+A_0B_1+A_1B_0+A_1B_1))\\ &=FWT(Merge(A_0B_0,A_0B_1+A_1B_0+A_1B_1))\\ &=FWT(C) \end{align} \]

小心 $Merge$ 的括号打的位置

第一个等号：按 FWT 定义展开

第二个等号：按 $\times$ 定义对应位相乘

第三个等号：利用归纳法得到的结论

第四个等号：把 $A_0B_0$ 理解成 $A^{\prime}_0$ , $A_0B_1+A_1B_0+A_1B_1$ 理解成 $A^{\prime}_1$

第五个等号：前文在定义 Merge 的后面一点点所述：

还知道 $C_0=A_0B_0$ ,$ C_1=A_0B_1+A_1B_0+A_1 B_1$

所以我们归纳证明了 $FWT(A)\times FWT(B)=FWT(C)$

IFWT

（小剧场）

FWT: 至高无上的 IFWT ！吾交给汝一个使命：干掉 $FWT(A) \times FWT(B) $ 之后出现在 $FWT(C_1)$ 中的 $FWT(A_0B_0)$ 项！主不需要它！

IFWT：（心里mmp：彩笔 FWT）哈哈哈！看我容斥！

~~（突然发现自己好智障）~~

直接给出来：

\[IFWT(A)=Merge(IFWT(A_0),IFWT(A_1-A_0)) \]

其中传入的 $A$ 是经历了 $FWT$ 的产物，小证一手：

$FWT(A)\times FWT(B)=FWT(C_0)+FWT(C_0+C_1)$

所以：

$IFWT(FWT(C_0)+FWT(C_0+C_1))=Merge(IFWT(FWT(C_0)),IFWT(C_0+C_1-C_0))=Merge(IFWT(FWT(C_0)),IFWT(FWT(C_1)))=C$

FWT 的本质

我们考虑 FWT 的代码怎么写，这里再嫖一张 pyb 的 ppt

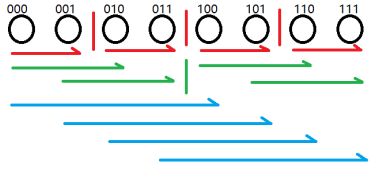
发现 $FWT$ 做的事情就是不断地让箭头的起点加到箭头的终点，按照红绿蓝的顺序一层一层地加，可以有代码：

void FWT(ll *A){
	for(int i=2;i<=N;i<<=1)         //i 线段长度
		for(int p=i>>1,j=0;j<N;j+=i)//j 哪一个部分
			for(int k=j;k<j+p;++k)  //k 嫖取信息
				A[k+p]+=A[k];
}

我们仔细观察这些箭头究竟都干了什么：

对于 $111$ 而言，它嫖走了 $110,101,011$ 的信息

对于 $110$ 而言，它嫖走了 $101,010$ 的信息

对于 $101$ 而言，它嫖走了 $100,001$ 的信息

对于 $100$ 而言，它飘走了 $000$ 的信息

你发现了吗？也就是说，每个位置获取的是它二进制少掉一个 $1$ 后的位置的信息

而在获取这些少掉了 $1$ 的位置的信息之前，这些少掉了 $1$ 的位置也获取了它们所需要的信息，所以，我们刚刚不是说 $FWT$ 可以看成一个“抽象函数”吗，它的“解析式”其实长这样：

\[FWT(A)_i=\sum_{j\subseteq i}a_j \]

$FWT(A)_i$ 表示 $FWT(A)$ 的第 $i$ 项，这里之所以用 $\subseteq$ 是因为 FWT 本身其实就是在解决“集合幂级数”。

可以带入 $FWT(A)\times FWT(B)$ 验证一下看是不是就是 $FWT(C)$

所以，我们也可以从另外一个角度去证明 FWT 的时间复杂度，即是 $\sum_{0}^{1<<n}popcount(i)=n2^{n-1}$

上面给出 $FWT$ 的代码，其实很容易写出 $IFWT$ 的代码：

void IFWT(ll *A){
	for(int i=2;i<=N;i<<=1)         
		for(int p=i>>1,j=0;j<N;j+=i)
			for(int k=j;k<j+p;++k)
				A[k+p]-=A[k];//唯一不同点
}

从代码逻辑的直观感受来看，如果我 FWT 的枚举顺序是 $i=2...N$，那 IFWT 的顺序是不是应该从 $i=N...2$ 才对？

正确性可以这样理解，FWT 本质是线性变化，所以每一个二进制其实挺独立的，也就是满足交换律。（没有必要是从低位到高位做，也可以是任意顺序做，只是这样写比较方便）

我们甚至也可以是随便点定一个排列 $p$，然后按照排列 $p$ 的顺序做。

更为直观的说明是，如果把每一个数字看成是一个 $F_2^n$ 空间的向量，每一个二进制位代表某一个维度的坐标，那么上面实际上做的就是高维前缀和。而高维前缀和自然可以随便钦定枚举维度的顺序，然后每次 $0\to 1$。

所以，我们容易把它整合起来：

void FWT(ll *A,int op){
	for(int i=2;i<=N;i<<=1)         //i 线段长度
		for(int p=i>>1,j=0;j<N;j+=i)//j 哪一个部分
			for(int k=j;k<j+p;++k)  //k 嫖取信息
				A[k+p]+=op*A[k];
}

上面从类似 FFT 的构造线性变化的角度出发，通过一点人类智慧，构造出了点值对应的形式，并证明了这样做是合法的。

但同时我们也发现 FWTor 其实就是高维前缀和的形式，而 IFWTor 就是高维差分，那么，我们能不能直接从高维前缀和/差分的角度来理解这样做 or 卷积的正确性呢？

我们考虑这个高维前缀和的形式：$F(S)=\sum _{T\subseteq S} f(T)$

我们说，与之对应的高维差分：$f(S)=\sum _{T\subseteq S} (-1)^{|S \backslash T|}F(T)$ 其实本质就是容斥原理：

\[f(S)=F(S)-(F(S) 中选的是 $S$ 的真子集的部分)=F(S)-(F(T),T 是 S 的 ppc(T)=ppc(S)-1 的子集)+（多个 T 重叠部分）=\dots \]

考虑我们的高维前缀和实际上解决的是这样的问题：对于两个不同的组合对象，从对象 1 中选出 $S$ 的方案数为 $f(S)$ ，从对象 2 中选出 $S$ 的方案数是 $g(S)$ ，我们想要计算的是 $(f*g)(S)=\sum _{T_1\cup T_2 = S}f(T_1)g(T_2)$ 的值

发现实际上能产生贡献的 $(T_1,T_2)$ 需要满足如下条件：

$T_1\subseteq S,T_2 \subseteq S$
$\forall x\in S , s.t. x\in T_1 \cup x\in T_2$

发现第一个条件是比较喜欢的，因为实际上它意味着所有在 $T$ 中的元素都在 $S$ 中，限制比较强烈

而第二个条件涉及到一个 $or$ 的问题，比较麻烦，我们考虑把这个条件容斥掉

条件的否定是： $\exist x\in S ,s.t. x\notin T_1 \and x\notin T_2$

考虑枚举 $S^{\prime }$ 使得 $\exist x\in S^{\prime}$ 满足上述条件，考虑此时 $T_1,T_2$ 满足的条件，有

\[\begin{align*} (f*g)(S)&=\sum_{S^{\prime}\in S} (-1)^{|S\backslash S^{\prime}|}\sum f(\subseteq S^{\prime}) \sum g(\subseteq S^{\prime})\\ &= \sum _{T\in S} (-1)^{|S\backslash T|}F(S)· G(S) \end{align*} \]

所以：$f∗g$ 为 $F⋅G$ 的高维差分，那么并卷积的高维前缀和为 $F⋅G$，即 $FWTor(f*g)=F·G$，$IFWT(F·G)=f*g$，而 $F=FWT(f),G=FWT(g)$。于是，我们从组合容斥的角度，说明了 FWT 的正确性，并了解了其高维前缀和/差分的本质。

下面是题外话，我们可以同样以这样高维前缀和/差分的思想去理解莫比乌斯反演，去理解 $\mu$ 到底是咋搞出来的。

莫比乌斯反演：

若 $g=1*f $ ，构造函数 $\mu$ ，使得 $1*\mu = \in$ ，有 $f=\mu *g$

写开：$g(n)=\sum _{d|n} f(d)$

考虑使用多元组来表示一个数，对于一个 $n=\prod p_i^{a_i}$ ，我们使用 $(a_1,a_2,\dots ,a_r)$ 来表达

重定义 $\subseteq$ 符号表示对于两个二元组 $(a_i) ,(b_i)$ ，若 $\forall i, a_i\le b_i$ ，那么 $(a_i)\subseteq (b_i)$

那么，可以表示成： $g(S)=\sum _{T\in S} f(T)$ ，其实就是高维前缀和

所以对应的反演形式，也就是 $f(n)=\sum _{d|n} \mu (\frac nd)g(d)$ ，可以看做是高维差分 $f(S)=\sum _{T\subseteq S} (-1)^{|S\backslash T|}g(T)$ ，而对应的 $\mu(n/d)=(-1)^{|S|-|T|}$

所以我们得以了解 $\mu$ 的构造思路！

想象现在我们在做二维差分 ,$a(i,j)=s(i,j)-s(i-1,j)-s(i,j-1)+s(i-1,j-1)$ ，系数都长成这样：

同理，考虑在刚刚所提到的表示法之下的系数，以 $x=2^i 3^j$ 为例子

$a(x)=s(x)-s(x/2)-s(x/3)+s(x/6)$ ，对应的 $\mu(1)=1,\mu (2)=-1,\mu(6)=1,\mu(合数)=0$

由此：

\[\begin{equation} \mu(N)= \left\{ \begin{array}{lr} 0,&\exist i\in[1,m],c_i>1\\ 1,&m\equiv 0(\bmod 2),\forall i\in[1,m],c_i=1\\ -1,&m\equiv 1(\bmod 2),\forall i\in[1,m],c_i=1\\ \end{array} \right. \end{equation} \]

FWTand

懒得写啦！所以直接摆式子

\[FWT(A)=\begin{cases} Merge(FWT(A_0+A_1),FWT(A_1))&,n>0\\ \quad\quad\quad\quad\quad\quad\quad A&,n=0 \end{cases}\\ IFWT(A)=(IFWT(A_0-A_1),IFWT(A_1))\\ FWT(A)_i=\sum_{i\subseteq j}a_j \]

注意到从某种意义上来说，$and$ 和 $or$ 是类似的，以为

$0|0=1,0|1=1,1|0=1,1|1=1$

$0\&0=0,0\&1=0,1\&0=0,1\&1=1$

void FWT(ll *A,int opt){
	for(int i=2;i<=N;i<<=1)
		for(int p=i>>1,j=0;j<N;j+=i)
			for(int k=j;k<j+p;++k)
				A[k]+=A[k+p]*opt;
}

类似上方对于 FWTor 的组合阐述，通过 Jzzhu and Numbers 这道题，我们也可以对 FWTand 做组合阐述。

现在有若干组合对象，$f_{1,\dots n}(s)$ 分别表示从这 $n$ 个组合对象里面选出集合 $s$ 的方案数，求有多少种选 $s_{1\dots n}$ 的方案，使得 $And_{i=1}^n s_i=0$。

方法是容斥，假如我求出了 $g[i]$ 表示 $And_{i=1}^n$ 的 $ppc\ge i$ 的方案数，那么 $ans=g[0]-g[1]+g[2]\dots$，（其实就等价于 IFWTand，只不过把 ppc 相同的先加在一起了）

$g[i]$ 的求法是容易的，只需要求出 $h[s]$ 表示 $s\subseteq And$ 的方案数，等价于对于每一个组合对象，都有 $s\subseteq s_i$。那么这个其实也就是 FWTand 转成点值然后对应位置相乘。

那么就做完了。

使用一点更为多项式的阐述：

\[\begin{align*} [x^{\varnothing}]\prod (1+x^{i})^{c_i}\\ &=[x^{varnothing}]IFWT(\prod FWT(1+x^i)^{c_i})\\ &=\sum_s (-1)^{|s|}[x^s](\prod FWT(1+x^i)^{c_i})\\ &=\sum_s (-1)^{|s|}\prod_{s\subseteq t} 2^{c_t}\\ &=\sum_s (-1)^{|s|}2^{\sum_{s\subseteq t}c_t} \end{align*} \]

所以这道题的做法就是先在 $\phi(mod)$ 下用 FWT 把 $2$ 的幂次做出来，然后带入上式。

FWTxor

其实 FWTxor 的推导过程才和 FFT 是最像的，怎么说呢？

显然有 $C_0=A_0B_0+A_1B_1$,$C_1=A_0B_1+A_1B_0$

FFT 的蝴蝶变换叫做：

\[F(\omega_n^k)=F_1(\omega_{\frac n2}^k)+\omega_n^kA_2(\omega_{\frac n2}^k)\\ F(\omega_n^{k+\frac n2})=F_1(\omega_{\frac n2}^k)-\omega_n^kA_2(\omega_{\frac n2}^k) \]

FWTxor 直接套用：

\[FWT(A)=\begin{cases} Merge(FWT(A_0+A_1),FWT(A_0-A_1))&,n>0\\ \quad\quad\quad\quad\quad\quad\quad A&,n=0 \end{cases} \]

然后你发现 $FWT(A)\times FWT(B)=Merge(FWT(A_0B_0+A_1B_1+A_0B_1+A_1B_0),FWT(A_0B_0+A_1B_1-A_0B_1-A_1B_0))$

然后你发现前半部分多了 $A_0B_1+A_1B_0$ ，后面部分需要多了 $A_0B_0+A_1B_1$ 而且还需要变个号

所以你灵光一现，如此构造出了 IFWT:

$IFWT(A)=Merge(IFWT(\dfrac{A_0+A_1}2),IFWT(\dfrac{A_0-A_1}2))$

然后你发现好像是解决了

void fwtxor(int *f,int op){
    for(int i=2;i<=len;i<<=1)
        for(int p=i>>1,j=0;j<len;j+=i)
            for(int k=j;k<j+p;++k){
                int x=f[k],y=f[k+p];
                f[k]=(x+y)%mod,f[k+p]=(x-y+mod)%mod;
                if(op==-1)(f[k]*=inv2)%=mod,(f[k+p]*=inv2)%=mod;
            }
}

然后你开始探究 FWTxor 的本质（“解析式”）

然后你懵逼了

然后你上网看了一下：

\[FWT(A)_i=\sum_{j=0}^n(-1)^{|j\cap i|}a_j \]

然后你尝试探究如何从 FWT 的递推式得到它，

然后你发现你想不明白，但是模拟一下它就是对的，于是你有上网一通乱找，你找到了 pyb‘s ppt 的参考文献

（其实一言以蔽之，考虑在 $F_2$ 下的乘法其实就是 $ppc(i&j)$，所以可以从 FFT 为什么对理解 FWT 为什么对）

当你看完了巨佬的文章，你开始尝试自己推导：

\[c_i=\sum_{j\oplus k=i}a_jb_k=\sum_{j\subseteq i}\sum_{k\subseteq i}[i\oplus j\oplus k=0]a_jb_k \]

这个时候你又知道这样一个式子：

\[\frac{1}{2^n}\sum_{T\subseteq U}(-1)^{|W\cap T|}=1\Leftrightarrow W=\empty \]

其中 $U$ 代表某一个大小为 $2^n$ 的全集，$W$ 是随便自己给定了一个集合

它的正确性是很显然的，当 $W$ 不为空的时候，显然会出现一些 $-1$ ，从而使得这个 $\sum$ 的值小于 $2^n$

当且仅当 $W$ 为空集的时候，才会使得这个 $\sum=2^n$

然后，你利用这个式子，进行你的推导

\[\sum_{j\subseteq i}\sum_{k\subseteq i}[i\oplus j\oplus k=0]a_jb_k=\sum_{j\subseteq i}\sum_{k\subseteq i}\frac1{2^n}\sum_{T\subseteq U}(-1)^{|(i\oplus j\oplus k)\cap T|}a_jb_k \]

你发现你的推导还需要一点东西，所以你来证明这个：

\[|T\cap\oplus_{i=1}^x s_i|\equiv \sum|T\cap s_i|\pmod2 \]

其中 $s_i$ 是某个集合，$T$ 是某个集合。

（注意，下面没有采用原博客所使用的方法）

我们直接把集合看成二进制（反正上面的文章也一直把集合和二进制在混用qwq) ，下面简记 $popcount\to ppc$

即证明 $ppc(i\&(j\oplus k))\equiv ppc(i\&j)+ppc(i\&k)\pmod 2$

~~（突然发现由于写了太多，导致上面出现了奇怪的人称变化）~~

设 $z=i\&(j\oplus k),x=i\&j,y=i\&k$ ，接下来分类讨论，对于二进制每一位，都有：

$x$ 当前位为 $0$ ，$y$ 当前位为 $0$ 。那么要么是 $i$ 没有当前位，要么是 $j,k$ 均没有当前位，所以 $z$ 当前位也是 $0$
$x$ 当前位为 $0$ ，$y$ 当前位为 $1$ 。那么肯定是 $j$ 没有当前位，$i,k$ 均有当前位，所以 $z$ 当前位也是 $1$
$x$ 当前位为 $1$ ，$y$ 当前位为 $0$ 。那么肯定是 $k$ 没有当前位，$i,j$ 均有当前位，所以 $z$ 当前位也是 $1$
$x$ 当前位为 $1$ ，$y$ 当前位为 $1$ 。那么肯定是 $i,j,k$ 均有当前位，$z$ 当前位为 $0$ ，在 $mod\ 2$ 意义下依旧满足

所以现在我们已经证明了 $x=2$ 的情况，容易发现 $n>2$ 的情况可以看成 $n=2$ 的情况，解决

所以我们现在继续我们的推式子大业：

\[\begin{align} \sum_{j\subseteq i}\sum_{k\subseteq i}\frac1{2^n}\sum_{T\subseteq U}(-1)^{|(i\oplus j\oplus k)\cap T|}a_jb_k&=\sum_{j\subseteq i}\sum_{k\subseteq i}\frac1{2^n}\sum_{T\subseteq U}(-1)^{|T\cap i|+|T\cap j|+|T\cap k|}a_jb_k\\ &=\frac1{2^n}\sum_{j\subseteq i}\sum_{k\subseteq i}\sum_{T\subseteq U}(-1)^{|T\cap i|}(-1)^{|T\cap j|}a_j(-1)^{|T\cap k|b}b_k \end{align} \]

顺理成章的，我们知道了：

\[FWT(A)_i=\sum_{j=0}^n(-1)^{|j\cap i|}a_j \]

！！！

「CF662C」 Binary Table

CF662C Binary Table - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

延续做一道黑题写一篇题解的传统，我们直接把题解写在这里面

Statement

有一个 $n$ 行 $m$ 列的表格，每个元素都是 $0/1$ ，每次操作可以选择一行或一列，把 $0/1$ 翻转，即把 $0$ 换为 $1$ ，把 $1$ 换为 $0$ 。请问经过若干次操作后，表格中最少有多少个 $1$ 。

$n\leq 20,m\leq 10^5$

Solution

注意到 $𝑛$ 很小

容易得到暴力算法：暴力枚举第 $𝑖$ 行是否翻转，这样每一行的状态就已确定，对于每一次完整的行翻转后，取每一列 $0/1$ 个数较小的贡献即可。（因为每一列也可以翻转）

时间复杂度是 $𝑂(𝑚 ⋅ 2^𝑛 )$ ，我们考虑优化掉这个 $m$

显然行的操作我们可以状压为 $𝑥$，（二进制为 $1$ 的位表示那一行要翻转）

每一列的的状态值也可以压缩：

用 $𝐴[𝑖]$ 表示在原表列中， $𝑖$ 这个状态数量
用 $𝐵[𝑖]$ 表示 $𝑖$ 这个状态最小 $1$ 的个数（即 $\min(popcount(i), n-ppc(i)$)

当确定了行的操作为 $x$ ，那么所有状态为 $i$ 的列的贡献为：$A[i]B[i\oplus x]$

令 $j=i\oplus x$ ，那么 $x=i\oplus j$

所以 $ans_x=\sum_{i\oplus j=x}A[i]B[j]$ ，直接上 FWT 即可

复杂度：$O(\max(n2^m,nm))$

Code

#include<bits/stdc++.h>
#define int long long
using namespace std;
const int N = (1<<21);
const int M = 1e5+5;

char s[25][M];
int a[N],b[N];
int n,m,ans=1e18;

void fwtxor(int *f,int op){
    for(int i=2;i<=(1<<n);i<<=1)
        for(int p=i>>1,j=0;j<(1<<n);j+=i)
            for(int k=j;k<j+p;++k){
                int x=f[k],y=f[k+p];
                f[k]=x+y,f[k+p]=x-y;
                if(op==-1)f[k]/=2,f[k+p]/=2;
            }
}

signed main(){ 
    scanf("%lld %lld",&n,&m);
    for(int i=1;i<=n;++i)scanf("%s",s[i]+1);
    for(int i=1,k;k=0,i<=m;++i,a[k]++)
        for(int j=1;j<=n;++j)k=k<<1|(s[j][i]-'0');
    for(int i=0,t;i<(1<<n);++i)
        t=__builtin_popcount(i),b[i]=min(t,n-t);
    fwtxor(a,1),fwtxor(b,1);
    for(int i=0;i<(1<<n);++i)a[i]*=b[i];
    fwtxor(a,-1);
    for(int i=0;i<(1<<n);++i)ans=min(ans,a[i]);
    printf("%lld\n",ans);
    return 0;
}

子集卷积

~~写不动了！！~~

https://www.luogu.com.cn/problem/P6097

所谓子集卷积，听着很高级，其实也就那样（就最基本的而言），好像有叫做集合占位幂级数什么的

它用来处理求出这样一个 $c$：

\[c_i=\sum_{\begin{align}j\ |\ k=i \\ j\ \&\ k=0\end{align}}a_jb_k \]

我们很容易处理第一个限制 $i \cap j=k$，直接 FWTand 即可。

对于第二个限制 $i \cap j=\varnothing\Leftrightarrow |i|+|j|=|i\cap j|$，所以我们不妨再开一维记录集合中的元素个数

也就是说设 $f_{i,j} = a_j[|j|=i],g_{i,j}=b_j[|j|=i]$，把他们卷起来，$h_{i,j}=\sum_{k=0}^i \sum_{l|r=j}f_{k,l}g_{i-k,r}$

最后的答案即为： $c_i=h_{|i|,i}$ ，因为 $popcount(i)+popcount(j)\ge popcount(i|j)$ ，所以相等的时候取到的就是正确的值

（即 $|S|+|T|=|S|T|+|S\&T|$ )

#include<bits/stdc++.h>
using namespace std;
const int N = 1<<21;
const int mod = 1e9+9;

int read(){
	int s=0,w=1;char ch=getchar();
	while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
	while(isdigit(ch))s=s*10+ch-'0',ch=getchar();
	return s*w;
}

int a[21][N],b[21][N],c[21][N];
int n,len;

void fwt(int *f,int op){
	for(int i=2;i<=len;i<<=1)
		for(int p=i>>1,j=0;j<len;j+=i)
			for(int k=j;k<j+p;++k)
				(f[k+p]+=op*f[k])%=mod; 
} 

signed main(){
	n=read(),len=1<<n;
	for(int i=0;i<len;++i)a[__builtin_popcount(i)][i]=read();
	for(int i=0;i<len;++i)b[__builtin_popcount(i)][i]=read();
	for(int i=0;i<=n;++i)fwt(a[i],1),fwt(b[i],1);
	for(int i=0;i<=n;++i)
		for(int j=0;j<=i;++j)
			for(int k=0;k<len;++k)
				(c[i][k]+=(long long)a[j][k]*b[i-j][k]%mod)%=mod;
	for(int i=0;i<=n;++i)fwt(c[i],-1);
	for(int i=0;i<len;++i)printf("%d ",(c[__builtin_popcount(i)][i]+mod)%mod);
	return 0;
}

所谓集合占位幂级数，是这样的形式：

\[f_Sg_T[S\&T=\varnothing]\to h_{S|T}\\ \sum_Sf_Sx^S\to \sum_S f_Sz^{|S|} x^S\\ fz^ax^S ·gz^bx^T\to fg\ z^{a+b}x^{S|T}\\ \]

扩展：https://www.luogu.com.cn/blog/user7035/zi-ji-juan-ji-ji-ji-gao-ji-yun-suan （我不会，等我长大后再学习）

[WC2018] 州区划分

WC2018 州区划分 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

延续做一道黑题写一篇题解的传统，我们直接把题解写在这里面

Statement

由于原题面已经概括得很好了，所以这里直接贴图:

$n\leq 21,m\leq n^2/2,p\le 2 ,w_i\le 100$

Solution

容易考虑状压 DP，设 $f[i][j]$ 表示划分了 $i$ 个州，选出的城市的集合为 $j$ 的贡献，那么

\[f[i][j]=\sum_{k\subseteq j}f[i-1][k](\dfrac{sum[k]}{sum[j]})chk[k] \]

其中，$sum[s]$ 表示集合 $s$ 的 $w$ 的和，$chk[s]$ 表示集合 $s$ 是否可以独立成州

所谓独立成州的条件其实可以转化为图不连通/存在奇度数点，我们容易在 $O(2^nm)$ 左右的时间暴力预处理出 $sum,chk$

设 $g[k]=sum[k]chk[k]$ ，那么：

\[\begin{align} f[i][j]&=\frac1{sum[j]}\sum_{k\subseteq j}f[i-1][k]g[k]\\ &=\frac1{sum[j]}\sum_{s\cup t=j \&\& s\cap t=\emptyset}f[i-1][s]g[t] \end{align} \]

发现后面的那一坨其实就是子集卷积，所以复杂度 $O(n^22^n)$ 解决

Code

#include<bits/stdc++.h>
#define int long long
#define ppc(x) __builtin_popcount(x)
using namespace std;
const int mod = 998244353;
const int N = 22;

char buf[1<<23],*p1=buf,*p2=buf;
#define getchar() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
int read(){
    int s=0,w=1; char ch=getchar();  
    while(!isdigit(ch)){if(ch=='-')w=-1;ch=getchar();}
    while(isdigit(ch))s=s*10+(ch^48),ch=getchar();
    return s*w;
}

int u[N*N],v[N*N],w[N],fa[N],deg[N],inv[(1<<N)+5];
int f[N][(1<<N)+5],g[N][(1<<N)+5];
int n,m,p;
bool vis[N];

void input(){
    n=read(),m=read(),p=read();
    for(int i=1;i<=m;++i)u[i]=read(),v[i]=read();
    for(int i=1;i<=n;++i)w[i]=read();
}
int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);}
bool merge(int u,int v){
    u=find(u),v=find(v);
    return u==v?0:fa[u]=v;//////////////
}
int ksm(int a,int b){
    int res=1;
    while(b){
        if(b&1)res=res*a%mod;
        a=a*a%mod,b>>=1;
    }
    return res;
}
void preparation(){
    for(int i=0,sum,cnt,flag;sum=cnt=flag=0,i<(1<<n);++i){
        for(int j=1;j<=n;++j)fa[j]=j,vis[j]=false,deg[j]=0;
        for(int j=0;j<n;++j)if(i&(1<<j))vis[j+1]=true,sum+=w[j+1],cnt++;
        for(int j=1;j<=m;++j)if(vis[u[j]]&&vis[v[j]])
            merge(u[j],v[j])&&(cnt--,1),deg[u[j]]++,deg[v[j]]++;
        flag|=cnt!=1,cnt=0;
        for(int j=1;j<=n;++j)cnt+=(deg[j]&1);
        flag|=cnt!=0,g[ppc(i)][i]=flag*ksm(sum,p);
        inv[i]=ksm(ksm(sum,mod-2),p);
    }
}
void fwtor(int *f,int op){
    for(int i=2;i<=(1<<n);i<<=1)
        for(int j=0,p=i>>1;j<(1<<n);j+=i)
            for(int k=j;k<j+p;++k)(f[k+p]+=(op*f[k]+mod)%mod)%=mod;
}
void work(){
    for(int i=0;i<=n;++i)fwtor(g[i],1);
    f[0][0]=1,fwtor(f[0],1);
    for(int i=1;i<=n;++i){
        for(int j=0;j<i;++j)//j!=i
            for(int k=0;k<(1<<n);++k)
                (f[i][k]+=f[j][k]*g[i-j][k]%mod)%=mod;
        fwtor(f[i],-1);
        for(int j=0;j<(1<<n);++j)
            f[i][j]=(ppc(j)==i)*(f[i][j]*inv[j]%mod);
        if(i^n)fwtor(f[i],1);
    }
}
void output(){
    printf("%lld\n",f[n][(1<<n)-1]);
}

signed main(){
    input();
    preparation();
    work();
    output();
    return 0;
}

「CF1034E」Little C Loves 3 III

Statement

给定 $n$ 和长度为 $2^n$ 的数列 $a_{0},a_{1}...a_{2^n-1}$ 和 $b_{0},b_1...b_{2^n-1}$，保证每个元素的值属于$ [0,3]$

生成序列 $c$，对于 $c_i$，有：

$c_i=\sum_{j|k=i,j\&k=0} a_j\times b_k$

求 $c_{0},c_1...c_{2^n-1}$，答案对 $4$ 取模。

$n\le 21$，时限 $\rm 1s$

Solution

显然，暴力 $O(n^22^n)$ 的子集卷积不可过，考虑利用 $\bmod 4$ 的性质

普通的，子集卷积为了取到正确的值，采用的方法可以理解为 DP 多设一维状态 ${|S|}$ ，使得我们加入了 $z^{|S|}$ 这一项

这里，我们让 $a_S=a_S\times 4^{|S|},b_T=b_T\times 4^{|T|}$ （鬼知道是怎么想到的！）

用 FWT 求出 $c$ 后，$x^{|S|}$ 项系数对 $4^{|S|+1}$ 取模，再除以一个 $4{|S|}$ 即可

解释：

集合占位幂级数是这样的形式： $\sum_S (f_S z^{|S|}x^S+\sum_{i>|S|}\sigma_{i,S}z^ix^S)$ 其中 $z$ 的取值是任意的， $\sigma $ 一般都取 $\rm 0$ ，$\sigma$ 意义是在于可能会在 $S$ 位置瞎 jb 转上一些不计入答案的贡献

而当我们把 $z$ 取到 $\rm 4$ ， $\bmod 4^{|S|+1}$ 干掉了后面那个 $\sum$ ，除 $4^{|S|}$ 相当于还原

于是这样快乐 FWT 即可，$O(n2^n)$

Code

#include<bits/stdc++.h>
#define int long long
using namespace std;

char s[1<<21|5],t[1<<21|5];
int f[1<<21|5],g[1<<21|5];
int n;

void fwt(int *f,int op){
    for(int i=2;i<=(1<<n);i<<=1)
        for(int p=i>>1,j=0;j<(1<<n);j+=i)
            for(int k=j;k<j+p;++k)f[k+p]+=op*f[k];
}

signed main(){
    scanf("%lld%s%s",&n,s,t);
    for(int i=0;i<(1<<n);++i)f[i]=(s[i]&15ll)<<(__builtin_popcount(i)<<1);fwt(f,1);
    for(int i=0;i<(1<<n);++i)g[i]=(t[i]&15ll)<<(__builtin_popcount(i)<<1);fwt(g,1);
    for(int i=0;i<(1<<n);++i)f[i]*=g[i]; fwt(f,-1);
    for(int i=0;i<(1<<n);++i)putchar(f[i]>>(__builtin_popcount(i)<<1)&3|48);
    return 0;
}

完结撒花！！！！✿✿ヽ(°▽°)ノ✿

posted @ 2022-01-08 23:07 _Famiglistimo 阅读(1454) 评论(0) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

lost_heart_hurts

FWT 学习笔记

FWT 学习笔记

FFT

FWT

FWTor

FWT

IFWT

FWT 的本质

FWTand

FWTxor

「CF662C」 Binary Table

Statement

Solution

Code

子集卷积

[WC2018] 州区划分

Statement

Solution

Code

「CF1034E」Little C Loves 3 III

Statement

Solution

Code

公告