Savitzky-Golay滤波器 推导整理

背景：

最近遇到传感器分辨率导致的噪音问题，这会直接影响到卡尔曼滤波的过程误差。这里选择采用Savitzky-Golay滤波器进行平滑处理。想着推导一下，更好的理解这个算法。

基础：

数字滤波器，卷积，QR分解，向量投影

Part1 最小二乘估计

Savitzky-Golay 滤波器的本质是基于最小二乘估计的有限数字滤波器。

最小二乘结构：

现有数据： X=[x_{1};x_{2};...;x_{m}] , Y=[y_{1};y_{2};...;y_{m}]

曲线拟合： Y\equiv X\theta （矛盾方程组）

拟合目标：寻找拟合参数 \theta ，使拟合误差最小。 arg \min_{\theta}{\left| \left| X\theta-Y \right| \right|_{2}}

用线性方程组和矩阵表示为：

写到这里，我们的运算过程为：矩阵 x 向量 = 向量

这里机智的小伙伴会发现，这不就是向量投影嘛：

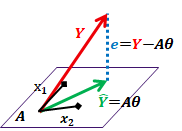
最小二乘估计变为：构建高维欧几里得空间，将向量Y进行投影，并使误差向量e的模最小。

这里定义A为列满秩实矩阵，那么根据上一篇QR分解文章有以下结论：

\hat{Y}=A\theta=A(A^{T}A)^{-1}A^{T}Y

A=QR

\theta=\left[ (QR)^{T}QR \right]^{-1}(QR)^{T}Y=R^{-1}Q^{T}Y

\hat{Y}=QQ^{T}Y

e=(I-QQ^{T})Y

%% Additional, Complexity level is 2mn^{2} flops

% QR factorization: 2mn^{2} flops

% Q^{T}Y product: 2mn flops

% R\theta=Q^{T}Y back substitution: n^{2} flops

Part2 Savitzky-Golay滤波器

Savitzky-Golay 滤波器的本质是基于最小二乘估计的有限数字滤波器。

取一段长度为2M+1的数字信号, 转移时间轴为中间位置:

采样时间： x=[-M;...;0;...;M]

信号幅值（后验）： Y=[y[-M];...;y[0];...;y[M]]

以N次多项式进行曲线拟合：

拟合关系：\hat{Y}= A\theta

参数向量 \theta ： \theta=[\theta_{0};...;\theta_{N}]

欧几里得高维空间矩阵A： A=[x.^{0},x.^{1},...,x.^{N}] (见图1)

估计向量（先验）： \hat{Y}=[\hat{y}[-M];...;\hat{y}[0];...;\hat{y}[M]]

估计向量中的元素： \hat{y}[n]=\theta_{0}(x[n])^{0}+...+\theta_{N}(x[n])^{N}

现在Recall Part1 向量投影知识：

误差向量 e=Y-A\theta 与空间矩阵A垂直时，e的模长最小，那么有： e\bot A

根据向量点积概念，有： A^{T}(Y-A\theta)=0 ，即 \theta=(A^{T}A)^{-1}A^{T}Y

那么我们对信号Y的先验估计为: \hat{Y}= A\theta=A(A^{T}A)^{-1}A^{T}Y

其中 A(A^{T}A)^{-1}A^{T} 为投影矩阵，这里记为P

那么对信号Y的先验估计可以简写为： \hat{Y}=PY

Y的先验估计有2M+1个，但现在只用x=0的估计数据：

降阶观测：\hat{y}[0]=P_{0th -row}*Y ， 其中 P_{0th -row} 为投影矩阵P的‘第0行’

改写为： \hat{y}[0]=\sum_{x=-M}^{M}{p_{0,x}}*y[x] （1）

这里机智的小伙伴又发现了， 怎么这么像卷积呢?

数字卷积： \hat{y}[n]=\sum_{x=n-M}^{n+M}{h[n-x]y[x]} （2）

n取0时，（1）与（2）相等，那么有： h[-x]=p_{0,x} ， -M\leq x\leq M

我们的卷积核就出来啦~

以上，就是Savitzky-Golay滤波器，是不是很简单呢~